Поверхности 2-го порядка: примеры

Опубликованно 05.10.2017 18:40

Поверхности студентка 2-го порядка встречается чаще всего в первый год. Первая задача на эту тему могут показаться простыми, но, как вы изучаете высшую математику и углубление в научные стороны, вы можете, наконец, перестать ориентироваться в происходящем. Для того, чтобы избежать подобной ситуации, необходимо не просто заучить, но и понять, как это один или другой поверхности, как изменение факторов, влияющих на нее, и его расположение относительно исходной системы координат и как найти новую систему (ту, в которой ее центр совпадает с осью симметрии, параллельной одной из координатных осей). Давайте начнем с самого начала. Определение

Поверхности 2-го порядка называется геометрическое место, чьи координаты удовлетворяют общему уравнению следующего вида:

Ф(Х,у,Z)=0.

Понятно, что каждая точка, принадлежащая поверхности должны быть три координаты в какой-либо определенной основе. Хотя в некоторых случаях геометрическое место точек может быть дегенератом, например, в самолете. Это лишь означает, что одна координата постоянна и равна нулю во всей области допустимых значений.

Польностью покрашенный форма вышеупомянутого равенства выглядит следующим образом:

В11х2+А22г2+А33з2+2А12ху+2А23ЮЗ+2А13хz+2А14х+2А24г+2А34З+А44=0.

Внм – некоторые константы, x, у, Z – переменные, соответствующие аффинные координаты любой точки. По крайней мере, один из множителей константы должны быть равны нулю, нет ни какого смысла бы в уравнение.

В подавляющем большинстве примеров числовых множителей равно тождественно равен нулю, и уравнение существенно упрощается. На практике, присвоение баллов на поверхность не составляет труда (достаточно подставить ее координаты в уравнение и проверить, является ли идентичность). Ключевым аспектом этой работы является приведение последнего к канонической форме.

Написанное выше уравнение определяет любые (все последующие) поверхности 2 порядка. Примеры будут рассмотрены далее.Типы поверхностей 2-го порядка

Уравнения поверхностей 2-го порядка отличаются только значениями коэффициентов внм. Общий вид при определенных значениях константы могут быть различные поверхности, классифицируются следующим образом:Цилиндры.Эллиптический Тип.Гиперболического типа.Конического типа.Параболического типа.Самолет.

Каждый из этих типов имеют естественную форму и мнимой: в воображаемой форме локуса материальных точек или вырождается в простую фигуру, нет.Цилиндры

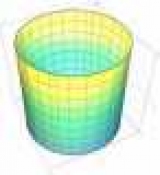
Это самый простой Тип, с относительно сложной Кривой лежит только в основе, выступая в качестве гида. Построение прямой, перпендикулярной к плоскости, в которой лежит база.

На графике показана круговой цилиндр является частным случаем эллиптического цилиндра. В XY-плоскости, ее проекция будет эллипсом (в нашем случае круг) направляет, и в xz – прямоугольник – как образующие параллельны оси Z. для того чтобы получить из общего уравнения, надо дать коэффициентов следующие значения:

Вместо привычного обозначения х, Y и Z используется х с серийным номером – это не имеет никакого значения.

На самом деле, 1/А -2 и другие, упомянутые здесь постоянные факторы, описанные в общее уравнение, но принято писать их в таком виде канонического представления. Далее, вы будете использовать исключительно такие записи.

Это устанавливает гиперболического цилиндра. Схема одна и та же гид будет гипербола.

г2=2 пикселя

Параболического цилиндра определяется несколько иначе: его каноническая форма включает в себя коэффициент р, называемый параметр. В самом деле, коэффициент равна Q=2Р, но решил разделить его на два множителя представлено.

Есть еще один вид баллонов: воображаемый. Этот цилиндр не принадлежит ни одной материальной точки. Он описывает уравнение эллиптического цилиндра, но вместо блок -1.Эллиптического типа

Эллипсоид может быть растянутым вдоль одной из осей (вдоль которых зависит от значений постоянных а, b, c, упомянутом выше; очевидно, что большой осью будет соответствовать более высокий коэффициент).

Кроме того, есть воображаемый эллипсоид, при условии, что сумма координат умножается на коэффициенты равны -1:

Гиперболоиды

Когда вы видите знак "минус" в одном из константы в уравнении эллипсоида превращается в уравнение однополостного гиперболоида. Вы должны понимать, что этот недостаток не должен быть в передней части x-координата3! Он лишь определяет, какая ось будет осью вращения гиперболоида (или параллельно с ней, как в появлении дополнительных слагаемых в квадрат (например, (х-2)2) смещается в центр фигуры, как следствие, на поверхности движется параллельно осям координат). Это касается всех поверхностей 2 порядка.

Кроме того, надо понимать, что уравнения, представленного в канонической форме и может быть изменен путем изменения констант (с сохранением знака!); тем не менее, их вид (гиперболоид, конус и т. д.) останутся прежними.

Это уравнение уже устанавливает duopolistic гиперболоид.

Коническая поверхность

В уравнении блок конуса не равен нулю.

Конус называется лишь ограниченное конической поверхностью. Картинка ниже показывает, что на самом деле, на графике будет два, так называемый конус.

Важное Примечание: во всех рассмотренных канонических уравнений константы принимаются по умолчанию положительное. В противном случае знак может повлиять на окончательное расписание.

Координатная плоскость стала плоскостью симметрии конуса, центр симметрии в начале координат.

В уравнение мнимого конуса не только преимущества, она имеет один единственный смысл.Параболоида

Поверхности 2-го порядка в пространстве может принимать различные формы, даже при схожих уравнений. Например, параболоиды бывают двух типов.

х2/А2+г2/Б2=2z паза

Эллиптический параболоид, с расположением оси Z, перпендикулярной чертежу будет проецируется в эллипс.

х2/А2-г2/Б2=2z паза

Гиперболический параболоид: в сечениях плоскостями, параллельными З. ы. будут параболы, а части плоскостей, параллельных ху – гипербола.

Пересекающиеся плоскости

Бывают случаи, когда поверхность 2-го дегенерата порядок в самолете. Эти самолеты могут быть расположены различными способами.

Во-первых, рассмотреть пересекающиеся плоскости:

х2/А2-г2/Б2=0

В этой модификации канонических уравнений получаются просто две пересекающиеся плоскости (воображаемой!); все физические точки, расположенные на оси координат, которая отсутствует в уравнение (в канонической – ось Z). Параллельные плоскости

г2=А2

Если есть только одна из координат поверхности 2-го вырождается в пару параллельных плоскостей. Не забудьте поставить Y может стоять любой другой переменной; затем, для получения плоскости, параллельной другой оси.

г2=?А2

В этом случае, они становятся мнимыми.Совпадающие плоскости

г2=0

В этого простого уравнения является пара вырожденных самолеты в одном – они одинаковы.

Не забывайте, что в случае трехмерного основании вышеизложенного уравнение задает линию y=0! Нет двух других переменных, но это просто означает, что их стоимость будет постоянно ноль.Дом

Одна из самых сложных задач для студентов является построение поверхностей 2-го порядка. Еще труднее переходить из одной системы координат в другую, с учетом углов наклона Кривой относительно осей и смещение центра. Давайте рассмотрим, как последовательно определить будущий вид чертежа аналитического метода.

Чтобы построить поверхность 2 порядка, необходимо:для приведения уравнения к каноническому виду;определить тип исследуемой поверхности;строить, исходя из значений коэффициентов.

Ниже представлены все типы:

Закрепить деталь в выписать один пример этого типа задание.Примеры

Предположим, мы имеем уравнение:

3(х2-2х+1)+6й2+2z паза2+60y+144=0

Привести его к каноническому виду. Выделить полные квадраты, т. е. skomponuem существующие компоненты так, чтобы они были разложения квадрата суммы или разности. Например: если (А+1)2=А2+2а+1, тогда2+2а+1=(А+1)2. Мы будем проводить вторую операцию. Квадратные скобки в данном случае не обязательно раскрывать, так как это только усложнит расчеты, но вынести общий множитель 6 (бандаж, полный квадрат Y) должен:

3(х-1)2+6(у+5)2+2z паза2=6

Переменной Z в этом случае имеет место только один раз – она еще не коснулась.

Проанализируем уравнение на данном этапе: перед всем неизвестным-это знак "плюс"; при делении на шесть-прежнему один. Таким образом, мы имеем уравнения, определяющего эллипсоид.

Обратите внимание, что 144 был выложен на 150-6, потом -6 сдвигается вправо. Зачем надо было так делать? Очевидно, самый большой делитель в данном примере составляет -6, что означает, что после деления на правый бок левый блок, необходимо "отложить" от 144 6 (о том, что право должно быть подразделение, наличие бесплатного термин константы, а не умноженное на неизвестное).

Мы разделили его на шесть и получаем каноническое уравнение эллипсоида:

(х-1)2/2+(г+5)2/1+з2/3=1

В ранее используемой классификации поверхностей 2-го порядка является особый случай, когда центром фигуры является источником. В этом примере, что-то сдвинулось.

Мы считаем, что каждый кронштейн неизвестен-новая переменная. То есть: а=х-1, Б=г+5, С=З. В новые координаты, центр эллипсоида совпадает с точкой (0,0,0), следовательно, А=B=C=0, где: х=1, У=-5, Z=0, и. В исходной координаты центра фигуры находится в точке (1,-5,0).

Эллипсоид будет получен из двух эллипсов: сначала в плоскости XY и второй плоскости xz (или УГ – неважно). Коэффициенты, которые являются переменными в канонической уравнение в квадрат. Таким образом, в приведенном выше примере, было бы лучше разделить на квадратный корень из двух, одного и квадратный корень из трех.

Чем меньше оси первого эллипса, параллельной оси Y, равен двум. Большой осью, параллельной оси х два корня из двух. Малые оси второго эллипса, параллельных оси Y остается неизменным – он равен двум. И большой осью, параллельной оси Z, равен двум корням из трех.

С помощью полученных из исходных уравнений путем преобразования к каноническому виду данные, которые мы можете нарисовать эллипсоид.Подводя итоги

Рассмотренные в этой статье, тема довольно обширная, но, на самом деле, как вы теперь видите, не очень сложно. Его развитие в основном заканчивается в тот момент, когда вы запоминаете имена и уравнений поверхности (и конечно, как они выглядят). В приведенном выше примере мы рассмотрели в деталях каждый шаг, но и приведение уравнения к каноническому виду требует минимальных знаний математики и не должно вызывать никаких затруднений у студента.

Анализ будущего графика на существующее равенство представляет собой более сложную задачу. Но хороших решений вы просто должны понять, как построить соответствующие кривые второго порядка – эллипсы, параболы и другие.

Случаи вырождения – еще проще раздел. Из-за отсутствия некоторых переменных для упрощения не только расчет, как уже упоминалось ранее, но и строить.

Как только вы сможете точно определить все типы поверхностей, варьировать постоянно, превращая графика в определенную форму – эта тема будет освоена.

Успехов в обучении!

Категория: Культура