Возражение-это... Определение, характеристика

Опубликованно 24.01.2019 13:00

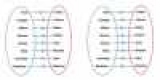
В математике есть понятие "множество", так как есть примеры сопоставления этих множеств между собой. Названия видов сопоставления набор действуют следующие слова: возражение, инъекции, коррекция. Ниже каждой иллюстрации подробнее.

Возражение-это... это что?

Группа элементов, первого сорта по сравнению со второй группой элементов из второго набора, таким образом: каждый элемент первой группы сопоставляется непосредственно с другим элементом второй группы, и, когда этого не происходит в ситуации отсутствия грубой силы или элементы любого из двух групп множеств.

Формулировка основных свойств: Элемент в один. Не остается лишних элементов при сопоставлении и сохранили первое свойство. Может быть, наоборот смотрите сопоставления с сохранением зрения. Возражение-это функция, которая также является простоя и творческой. Возражение с научной стороны

Цель функции-это я первая в категорию "ряд, и ряд функций". Однако зверь не всегда я первая более сложных категорий. Например, в определенной категории группы морфина должны быть мишки, так как они должны сохранить структуру группы. Так что я первая группа, которую я перед одноименной.

Понятие "взаимно-однозначное соответствие" обобщенной функции, разделяемые, в, которой называются частичные возражения, даже если частичное возражение-это то, что должно быть инъекции. Причина этого расслабления является то, что частично (необходимая) функция не определена для части своей области. Таким образом, нет никаких веских оснований для того, чтобы ограничить его функции обратного полной, т. е. некоторое во всем мире в своей области. Множество всех частичных клюв в этот набор называется диска перевернутой группа.

Другой способ определения той же концепции: а именно, что частичное возражение набор от a до B отношения R (функция частично) с тем свойством, что R-это графа против f:E'?B', где А' является подмножеством A и B' является подмножеством B.

Когда частичное возражение находится на том же наборе, иногда называется частичное преобразование "один к одному". Примером является преобразование Мебиуса, только, конечно, на комплексной плоскости, а не его завершение в расширенная комплексная плоскость. Инъекции

Группа элементов, первого сорта по сравнению со второй группой элементов из второго набора, таким образом: каждый элемент первой группы по сравнению с другой элемент второго, но не все они преобразуются в крутящий момент. Количество ни мяса элементов зависит от разницы между количеством этих элементов в каждом из наборов: если набор состоит из тридцати одного элемента, а другой на семь больше, количество ни мяса элементов - семь. Mira впрыска во многих. Возражение и инъекции похожи между собой, но не больше, чем просто похожи. Исправить

Группа элементов, первого сорта по сравнению со второй группой элементов из второго набора, таким образом: каждый элемент группы в виде пара, даже если существование разницы между количеством элементов. Отсюда следует, что элемент группы может создать пару с несколько элементов из другой группы. Ни цели, ни простоя, ни куритиба функции

Эта функция цель и творческого вида, но с остаточным элементом (ни мяса) => впрыска. Такая функция, очевидно, присутствует связь между зверь и коры, так как она непосредственно включает в себя данные два типа сопоставления набор. Здесь собраны все виды данных функций не является ни одним из них в отдельности. Объяснение всех видов функций

Например, заядлый наблюдатель следующие. Соревнования по стрельбе из лука. Каждый из участников хочет, чтобы поразить цель (для того, чтобы облегчить задачу: то, где падает стрелка, не принимается во внимание). Всего лишь три члена и три мишени-это первое поле (участок) для проведения турнира. В последующих разделах сохраняется количество лучников, но меняется количество целей: на втором - четыре цели, на следующем - еще четырех, а в четвертом - пять. Каждый участник стреляет по любой цели. Первая платформа для проведения турнира. Первый стрелок поражает только одну цель. Второй падает только в одну цель. Третий повторяет за другим, и все лучники попали в разные цели: те, что находятся перед ними. В конце концов, 1 (первый лучник) попали в цель (и), 2 (б) 3 (в). Наблюдается следующее соотношение: 1 – (a), 2 (b), 3 – (в). Заключением будет суждение о том, что сопоставление набор возражение. Вторая площадка для проведения турнира. Первый стрелок поражает только одну цель. Второй попадает в одну цель. Третий поправлю и повторяет все за другим, но условие то же - все лучники попали в разные цели. Но, как было сказано ранее, на втором этаже уже четыре мишени. Зависимость: 1 - (a), 2 (b), 3 - (в), (г) - ни мяса элемента набора. В этом случае, результат будет суждение о том, что сопоставление set - инъекции. Третье поле для турнира. Первый стрелок поражает только одну цель. Второй-войти еще раз в одну только цель. В третьем он решает взять себя в руки и поражает третий и четвертый цель. В конце концов, зависимость: 1 - (a), 2 (b), 3 - (в), 3 - (g). Здесь результат будет суждение о том, что сопоставление набора это исправить. Четвертое поле для турнира. С первым уже все понятно, поражает только одну цель, к которой скоро не будет места, чтобы уже скучно попаданий. Теперь второй берет на себя роль другого недавнего третьего и снова вступает в одной цели, повторяя первый. Третий продолжает держать в руке и не перестает знакомить его со стрелкой, с третьей и четвертой мишени. Пятый, однако, он все же оказался не подвержен. Таким образом, зависимость: 1 - (a), 2 (b), 3 - (в), 3 - (g), (d) - ни мяса элемента набора целей. Вывод: это сопоставление набора - не исправить, не инъекции и не возражение.

Теперь построить клюв, инъекции или становись взрослым не будет проблемой, так как найти различия между ними. Автор: Марадона Кирилл 2 Ноября 2018 года

Категория: Культура