Определение призмы, ее элементы и виды. Основные характеристики форм

Опубликованно 07.03.2019 01:30

Стереометрия - раздел геометрии, который изучает фигуры, которые не находятся в одной плоскости. Объектами изучения стереометрии являются призмы. В статье дадим определение призмы геометрической точки зрения, а также кратко перечислим свойства, которые в особенности. Геометрические фигуры

Определение призмы, геометрии, звучит следующим образом: это пространственная фигура, состоящая из двух идентичных n-угольники, расположенные в параллельных плоскостях, соединенных друг с другом вершинами.

Получить призма была не работа. Представьте себе, что есть два идентичных n-угольник, где n-число сторон или вершин. Поставим их так, чтобы они были взаимно параллельны. После этого, вершины многоугольника, вы должны связаться с вершинами другого. Образованная фигура будет состоять из двух n-уголь сторон, которые называются базами, и быть крутым сторон, которые представляют в целом, параллелограммы. Все параллелограммы форме боковой поверхности формы.

Существует другой способ геометрической приема вопрос о форме. Таким образом, если вы берете n-угольник, и осуществить ее перевод в другую плоскость с помощью параллельных сегментов одинаковой длины, а затем в новый план, мы получаем исходный многоугольник. Два многоугольника, а отрезки, параллельные, проведенные с их вершин, образуют призму.

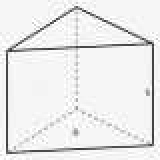
На рисунке выше показана треугольной призмы. Так она называется потому, что ее мотивы представляют собой треугольники. Элементы, которые составляют рисунок

Выше было дано определение призмы, из которого понятно, что основные элементы на рисунке, граней или сторон, ограничения всех точек призмы от внешнего пространства. Все лицо соответствующим фигура принадлежит к одному из следующих двух типов: сбоку; фонда.

Боковые части n, и они параллелизма или частных видов (прямоугольники, квадраты). В целом, боковые грани отличаются друг от друга. Грани основания только два, они представляют собой n-угольники и другой равны. Таким образом, каждая призма имеет n+2 частей.

Помимо сторон, рисунок отличается от своих вершин. Они представляют собой точки, где сходятся одновременно три грани. Две из трех граней всегда принадлежат боковой поверхности, и база. Таким образом, в колоде не специально выделенные вершины, как, например, в пирамиде, все они равны. Количество вершин фигуры равна 2*n (n штук в каждой базе).

Наконец, третий важный элемент призмы своих берегов. Это отрезки определенной длины, которые образуются путем пересечения части рис. Как грани, ребра также имеют два различных типа: либо формируется только боковыми сторонами; или происходят на стыке параллелограмм и стороны n-угольного основания.

Число ребер, таким образом, равна 3*n и 2*n из них принадлежат ко второму из этих типов. Типы призм

Различают несколько способов классификации призм. Но все они основаны на двух особенностей фигуры: на тип n-угольного основания; на боковой части.

Для начала, перейдем ко второй особенности и дать определение призмы, наклонной и прямолинейной. Если одна сторона parler a mon, рисунок называется наклонной, или что это. Если все параллелограммы являются прямоугольники или квадраты, призма является прямой.

Дать определение призмы, линия может также быть немного по-другому: справа от фигуры призмы, в которых кромки и боковые грани перпендикулярны его основаниям. На рисунке показаны два четырехугольные фигуры. Слева прямой, справа - склон.

Теперь мы перейдем к классификации по типу n-угольника, лежащего в фундаменте. Он может иметь те же стороны и под разными углами. В первом случае многоугольник называется правильным. Если этот рисунок содержит в основании многоугольник с равными сторонами и углами прямо, можно сказать, что он является правильным. В соответствии с этим определением, правильной призмы, в основании может быть равносторонний треугольник, квадрат, правильный пятиугольник или шестиугольник и так далее. Перечисленные формы правильные, показанные на рис.

Линейные параметры призмы

Для описания размеров рассматриваемых форм используют следующие параметры: высота; доля фонда; длина боковых ребер; объемные диагонали; диагонали боковых сторон и основания.

Для призмы всех величин связаны друг с другом. Например, длины боковых ребер одинаковы и равны высоте. Конкретной n-угольной правильной формы существуют формулы для двух линейных параметров, чтобы определить все другие. Поверхность рис.

Если вы достигаете данного выше определения призмы, а затем понять, что представляет собой площадь фигуры, это довольно легко. Поверхность-это поверхность всех граней. Для прямой призмы, она рассчитывается по формуле:

S = 2*So + Po*h

где So - площадь основания, Po - периметр n-угольника в основании, h - высота (расстояние между основаниями). Объем рис.

Параллельно поверхности, на практике важно знать объем призмы. Определить его можно по формуле:

V = So*h

Это справедливо для абсолютно любой призмы, в том числе тех, кто полулежа, формируются и неправильные многоугольники.

Для призмы объем в зависимости от длины базы и высоты формы. Для n-угольной призмы по формуле V-это особый тип. Автор: Валерий Савельев 26 Ноября 2018 Года

Категория: Культура