Уравнение плоскости. Угол между двумя плоскостями

Опубликованно 15.07.2019 02:55

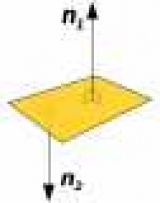
Самолет, вместе с точкой и прямой-это основной геометрический элемент. Используя его причине многие фигуры в трехмерной геометрии. В данной статье рассмотрим вопрос о том, как между двумя плоскостями угол найти. Концепция

Прежде чем говорить об угле между двумя плоскостями, это хорошо, чтобы понять, какой элемент геометрии будет обсуждаться. Разберемся в терминологии. Самолет-это бесконечный набор точек в пространстве, соединив их, мы получим вектор. Последний будет в отношении одного вектора перпендикулярны. Это называется перпендикуляром к плоскости.

На рисунке выше показан самолет и два вектора нормали к ней. Очевидно, что не лежат на одной прямой векторов. Угол между ними составляет 180часов. Уравнение

Между двумя плоскостями угол можно определить, если вы знаете математические уравнения рассматриваемых геометрических элементов. Существует несколько типов таких уравнений, названия которых перечислены ниже: общего типа; вектор; в сегментах.

Эти три являются наиболее удобными в решении различного рода проблем, поэтому они чаще всего используются.

Уравнение общего вида следующим образом:

А*х + В*У + С*З + Д = 0.

Здесь Х, Y, Z - координаты произвольной точки, принадлежащей этой плоскости. Параметров а, B, C и D представляют собой числа. Удобство этого обозначения состоит в том, что числа a, b, с-координаты нормального к плоскости вектора.

Векторная форма плоскости может быть представлен следующим образом:

х, у, Z) = (Х0, У0, г0) + ?*(А1, Б1, к.1) + ?*(А2, Б2, с2).

Здесь (а2, Б2, с2) а (а1, Б1, к.1) - параметров двух векторов координат, которые относятся к рассматриваемой плоскости. Точка (х0, У0и z0) также лежит в этой плоскости. Параметры ? и ? могут принимать независимые друг от друга и произвольные значения.

Наконец, уравнение плоскости в отрезках, чтобы представить следующей математической форме:

х/п + г/М + Г/Л = 1.

Здесь p, q, и L представляет собой определенное количество (включая отрицательные). Это уравнение полезно, когда вы хотите изобразить в прямоугольной системе координат плоскость, так как числа Р, Q, л показать точки пересечения с осями X, Y и Z самолета.

Обратите внимание, что каждое уравнение можно конвертировать в любой другой, используя простые математические операции. Формула угла между двумя плоскостями

Теперь рассмотрим следующий нюанс. В трехмерном пространстве две плоскости могут располагаться только в двух направлениях. Либо пересекаться или быть параллельными. Между двумя плоскостями называется угол, расположенный между их скольжения векторов (нормальный). Пересекающиеся вектора 2 образуют 2 угла (острый и тупой в общем случае). Так как угол между плоскостями считается острой. Рассмотрим уравнение.

Формула угла между двумя плоскостями:

? = arccos(|(П1*п2)|/(|Н1|*|н2|)).

Нетрудно догадаться, что это выражение является прямым следствием скалярное произведение нормальных векторов в N1 и N2 для рассматриваемых самолетов. Модуль скалярное произведение в числителе показывает, что угол ? будет принимать только значения от 0О до 90о. Изделия из модулей нормальных векторов в знаменателе означает, что продукт их длины.

Заметим, что если (П1*п2) = 0, то плоскости пересекаются под прямым углом. Пример задачи

Понимание того, что называется углом между двумя плоскостями, решить следующую проблему. В качестве примера. Итак, вам нужно вычислить угол между этими плоскостями:

2*х - 3*у + 4 = 0;

(х, у, Z) = (2, 0, -1) + ?*(1, 1, -1) + ?*(0, 2, 3).

Чтобы решить проблему, нужно знать векторы направления самолетов. К первой плоскости нормальный вектор составляет: N1 = (2, -3, 0). Чтобы найти второй плоскости нормальный вектор, умножение вектора, который появляется после параметров ? и ?. Результатом является вектором: N2 = (5, -3, 2).

Определить угол ?, мы используем формулу из предыдущего пункта. Получил:

? = arccos (|((2, -3, 0)*(5, -3, 2))|/(|(2, -3, 0)|*|(5, -3, 2)|)) =

= arccos (19/?(13*38)) = 0,5455 счастлив.

Расчетный угол в радианах соответствует 31,26вывода. Таким образом, самолет приведен в постановке проблемы пересекаются под углом 31,26вывода.

Валерий Савельев

Категория: Культура